当前位置：首页 > news >正文

做网站前台步骤百度权重怎么提高

news 2025/7/2 22:38:59

做网站前台步骤,百度权重怎么提高,专业做装修设计的网站,中国做外贸的网站目录定义推导前言证明定义高斯公式又叫高斯定理 (或散度定理）： 矢量穿过任意闭合曲面的通量等于矢量的散度对闭合面所包围的体积的积分它给出了闭曲面积分和相应体积分的积分变换关系，是矢量分析中的重要恒等式。推导前言 1.也…

定义

推导前言

证明

定义

高斯公式又叫高斯定理 (或散度定理）： 矢量穿过任意闭合曲面的通量等于矢量的散度对闭合面所包围的体积的积分 它给出了闭曲面积分和相应体积分的积分变换关系，是矢量分析中的重要恒等式。

推导前言

1.也就是封闭曲面通量问题，一块光滑连续的封闭曲面∑，围成一个几何体Ω，存在矢量场V，坐标不同，流速度不同

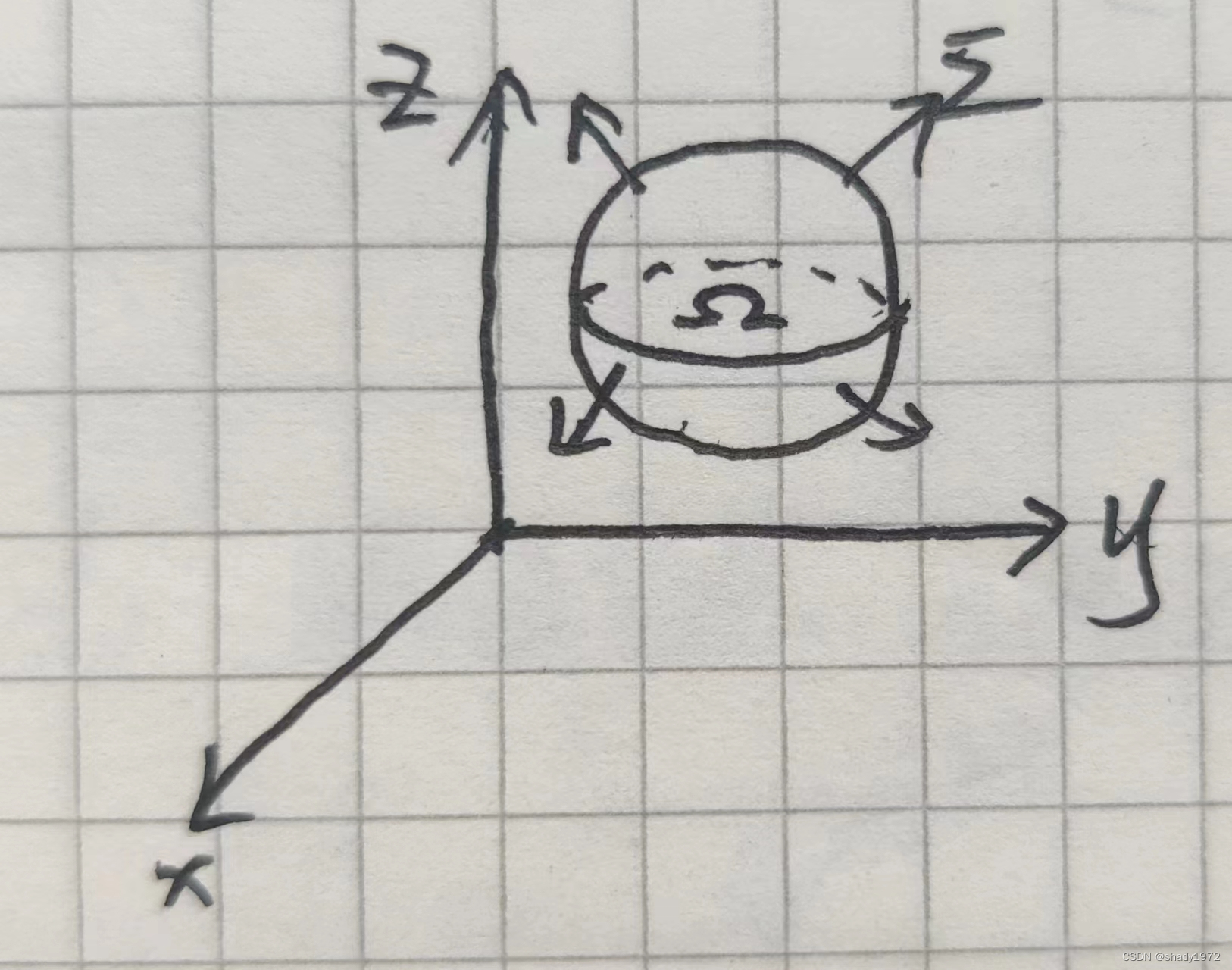
2.那么通过经典的积分思想：把∑分成无数小块，每块近似平面，且小块面上速度V近似不变，求出每一块通量再求和取极限，问题就能解决

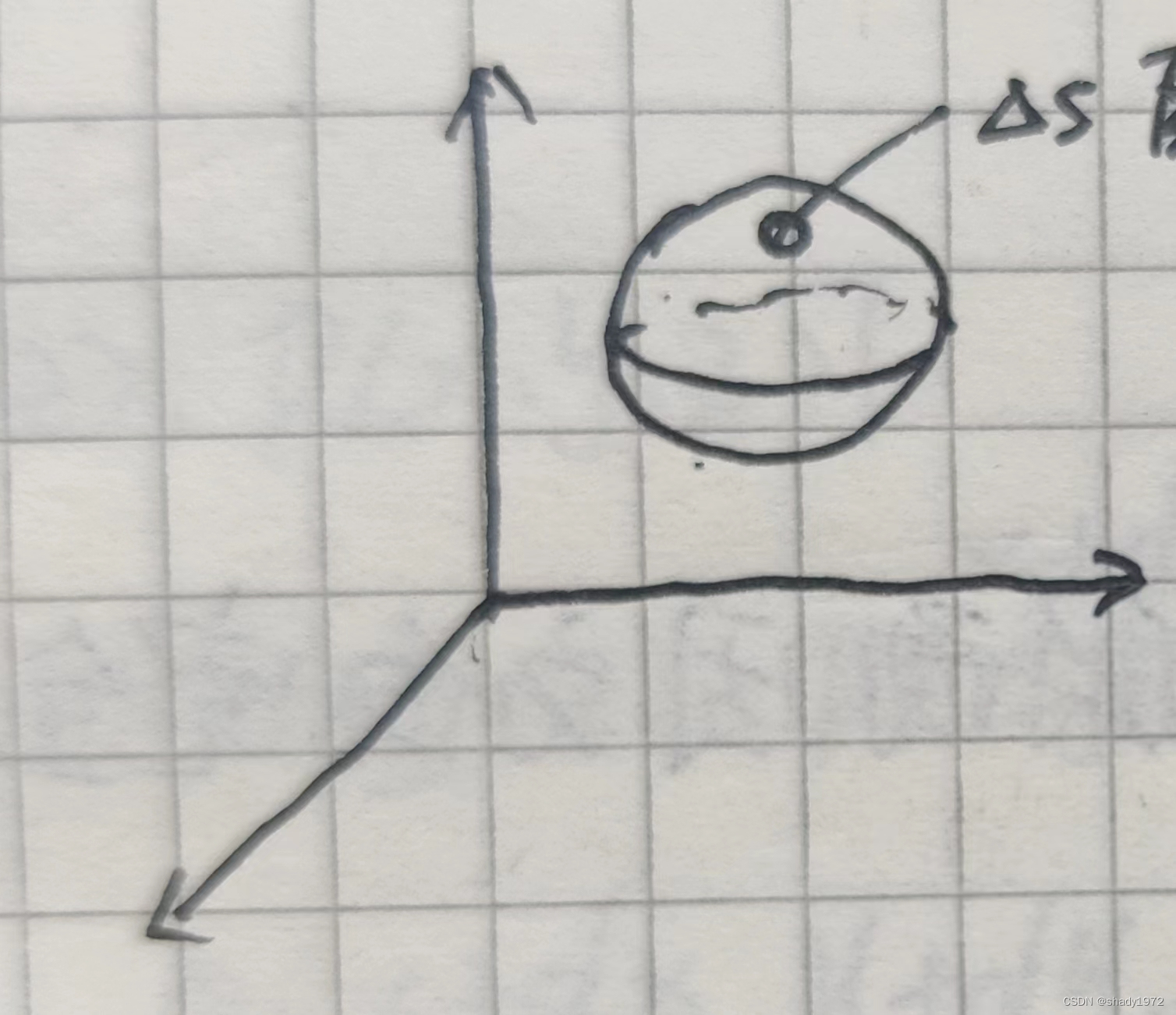
3.同样因为V的方向和Δs方向不一样，且夹角位置，所以把V分解为分别沿x,y,z方向，将Δs投影到三面得到x,y,z面对应的面积

那么总通量就得出为

一般做法将其换为二重积分进行计算，但是也有换不了的情况，那么高斯公式就能解决这一情况

证明

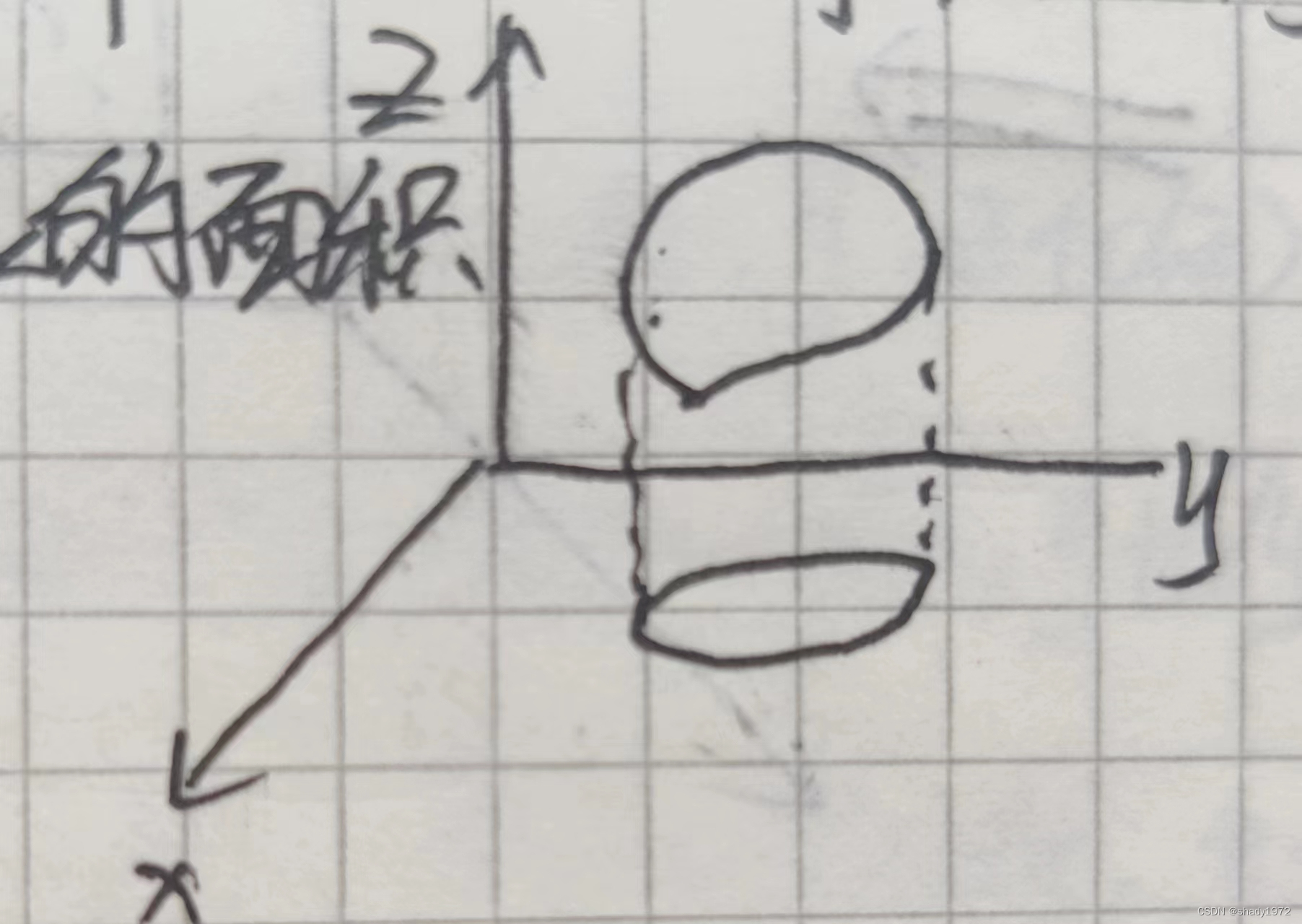
首先化繁为简，假设是计算一个矩形的通量

试着把两个矩形拼在一起

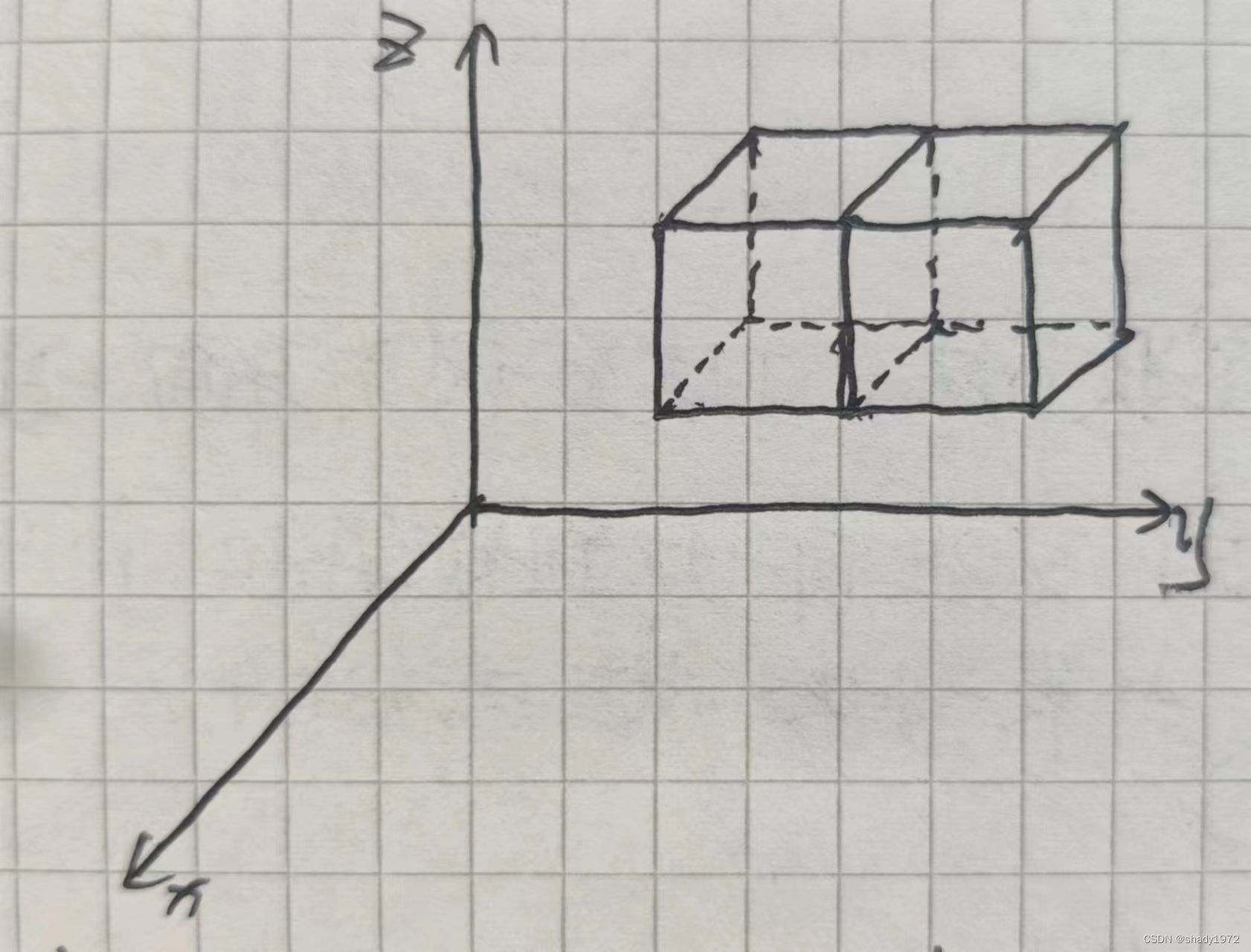
就会发现两个矩形重合的面因为方向完全相反，所以通量抵消，于是就可以简化

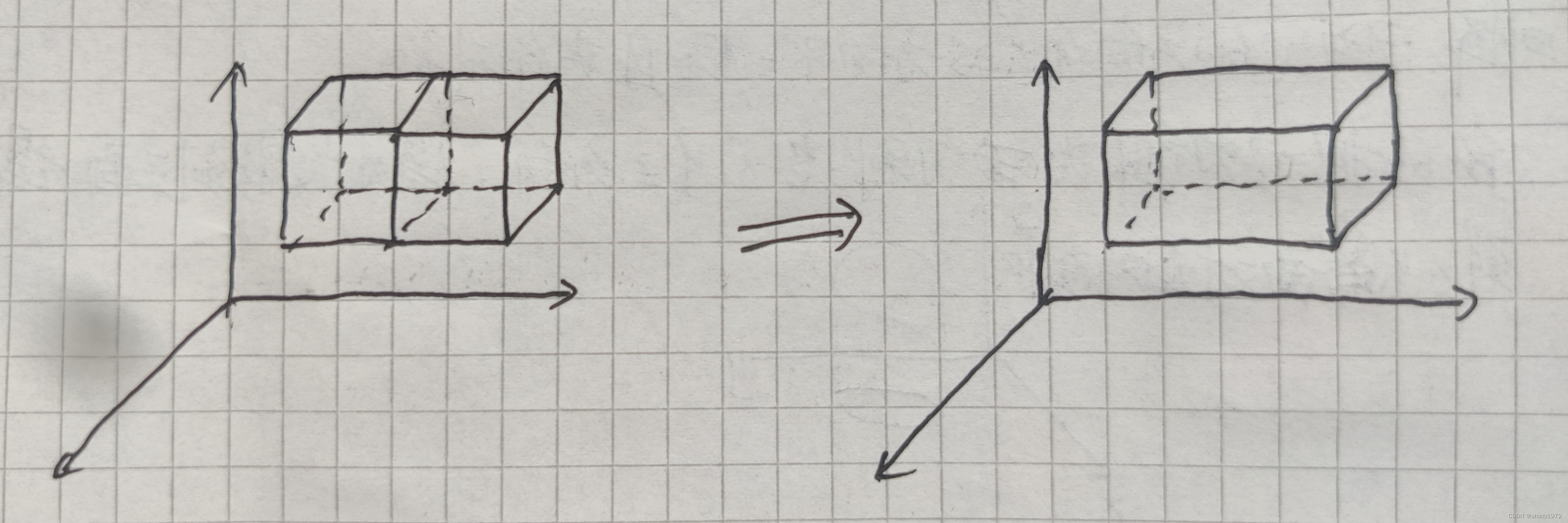
按照规律不管叠加多少个，都只会剩下外层

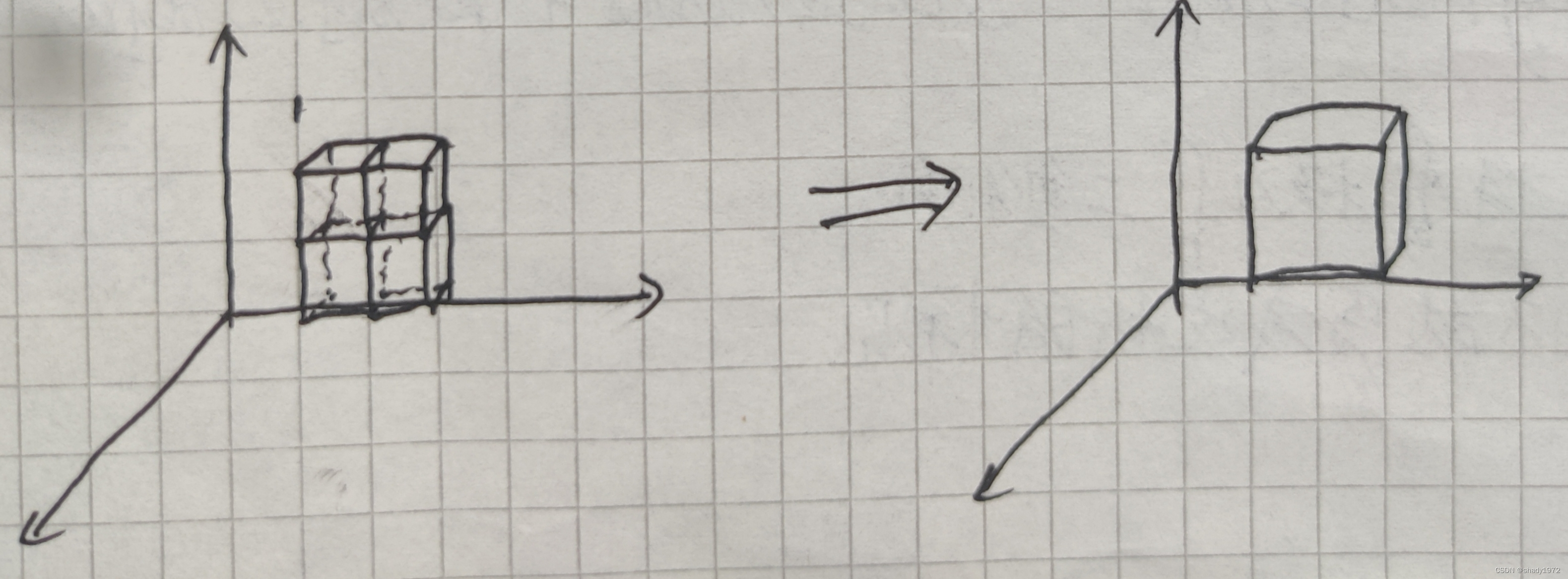
再加上积分的思想，就可以求出任何封闭曲面的通量了

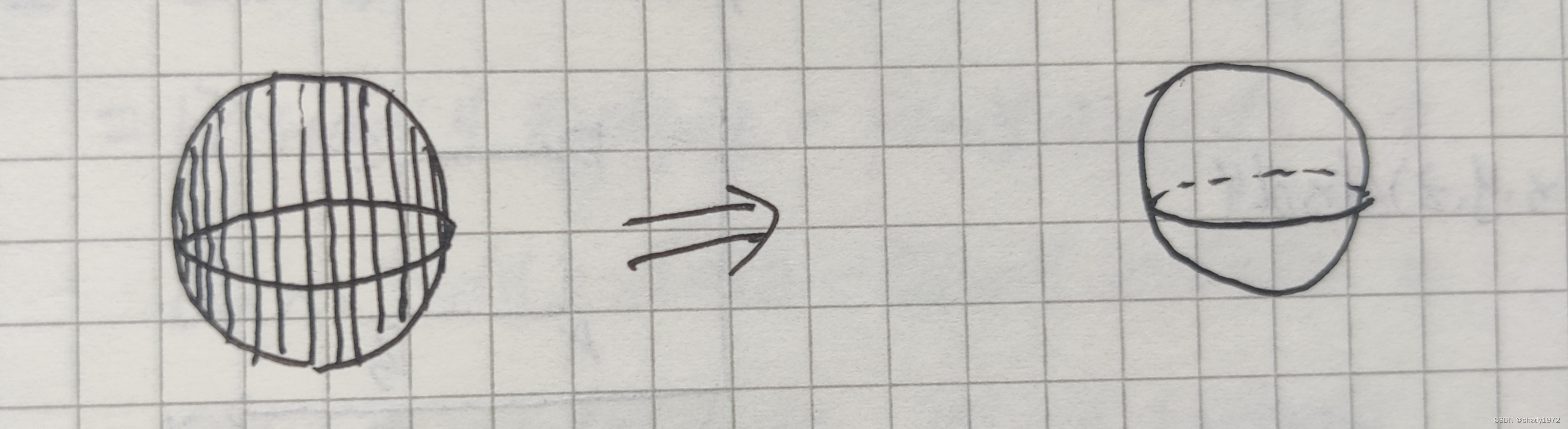
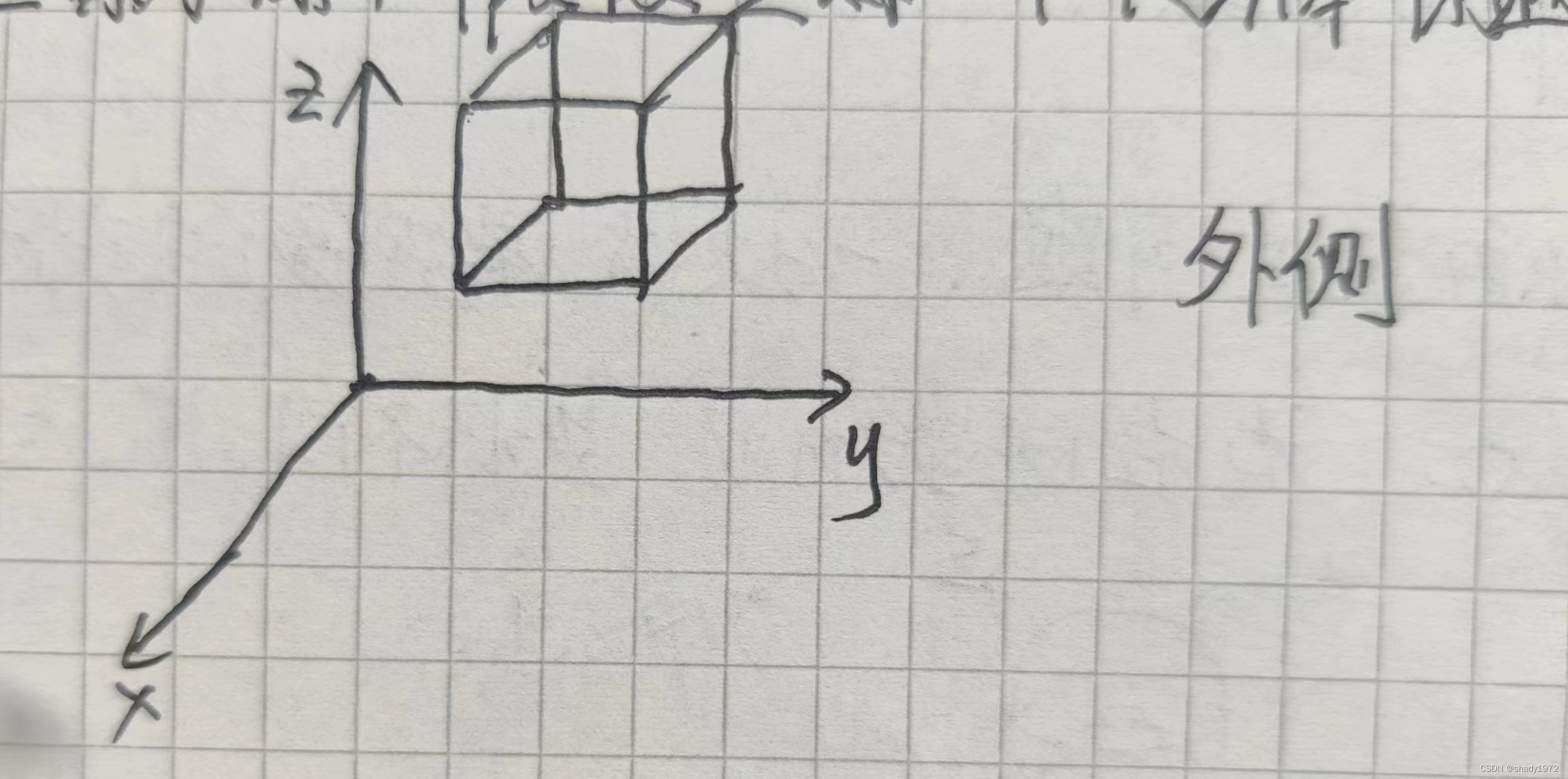
那么接下来开始公式的推导

取一小块dv，标注各点x,y,z方向的流速，外侧

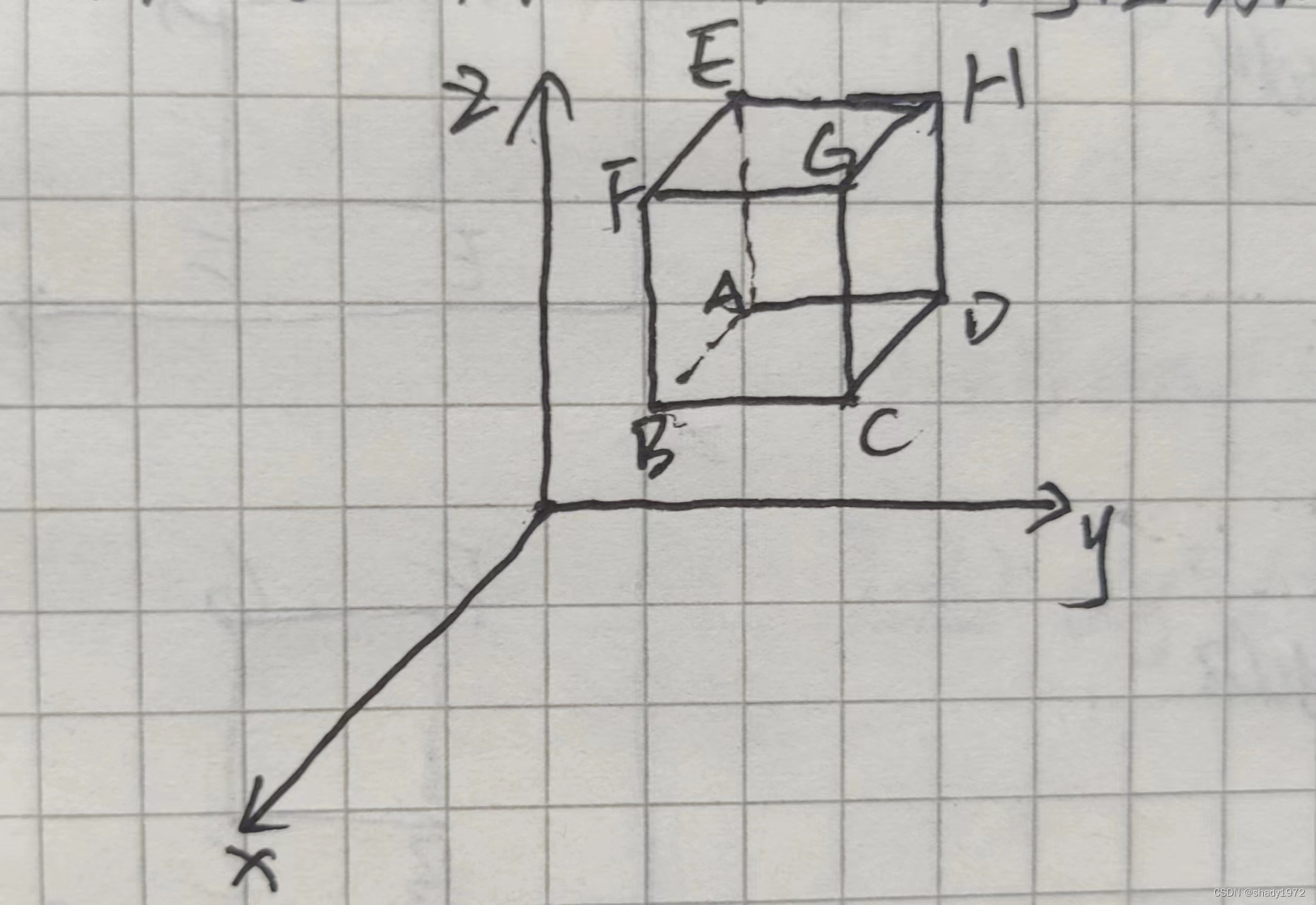
其中以A为基准

A[P(x,y,z)，Q(x,y,z)，z(x,y,z)]

B[P(x+dx,y,z)，Q(x+dx,y,z)，z(x+dx,y,z)]

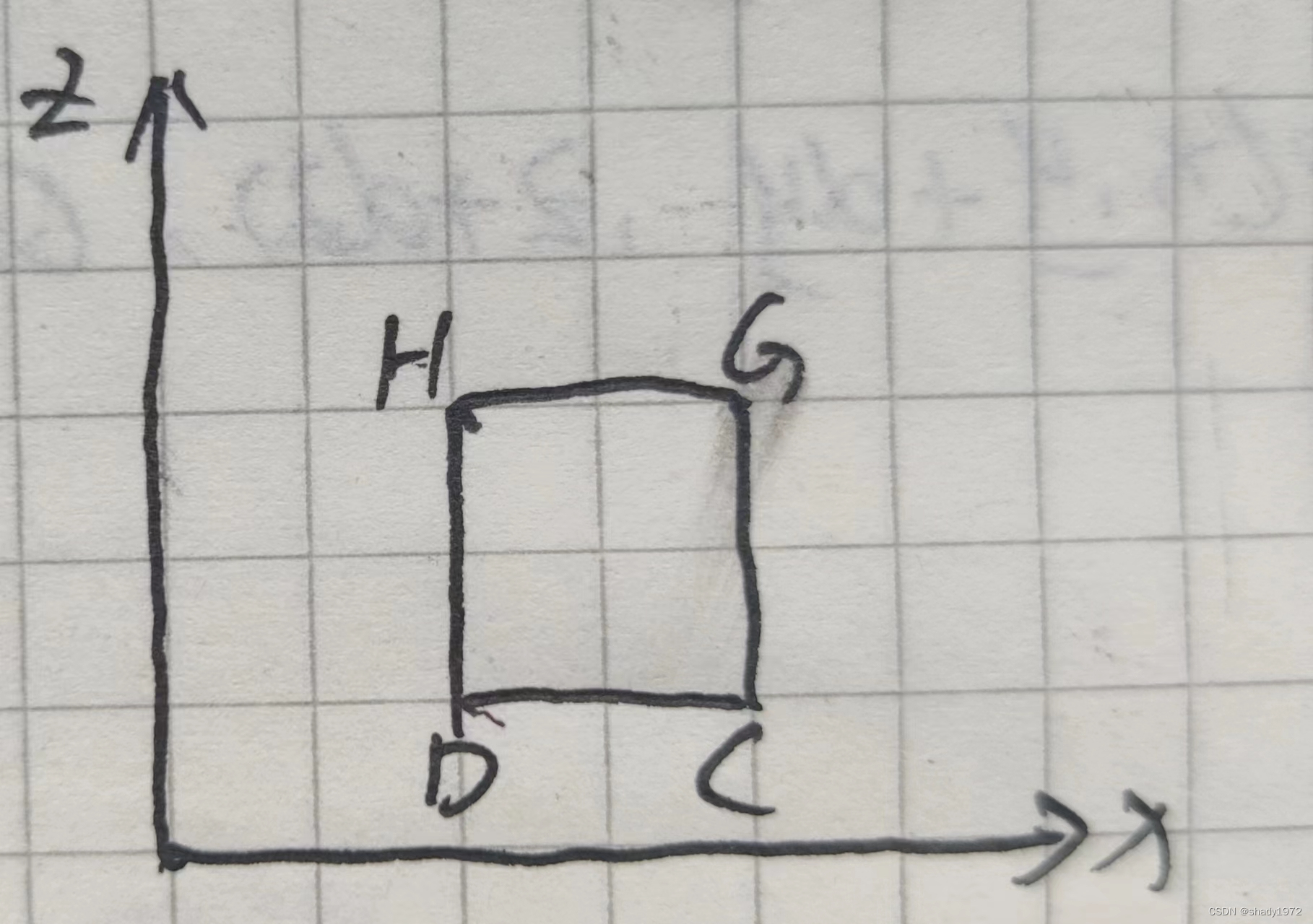
C[P(x+dx,y+dy,z)，Q(x+dx,y+dy,z)，z(x+dx,y+dy,z)]

D[P(x,y+dy,z)，Q(x,y+dy,z)，z(x,y+dy,z)]

E[P(x,y,z+dz)，Q(x,y,z+dz)，z(x,y,z+dz)]

F[P(x+dx,y,z+dz)，Q(x+dx,y,z+dz)，z(x+dx,y,z+dz)]

G[P(x+dx,y+dy,z+dz)，Q(x+dx,y+dy,z+dz)，z(x+dx,y+dy,z+dz)]

C[P(x,y+dy,z+dz)，Q(x,y+dy,z+dz)，z(x,y+dy,z+dz)]

那么就可以计算出各面通量

$\Phi$ ABCD = -R(x,y,z)dxdy

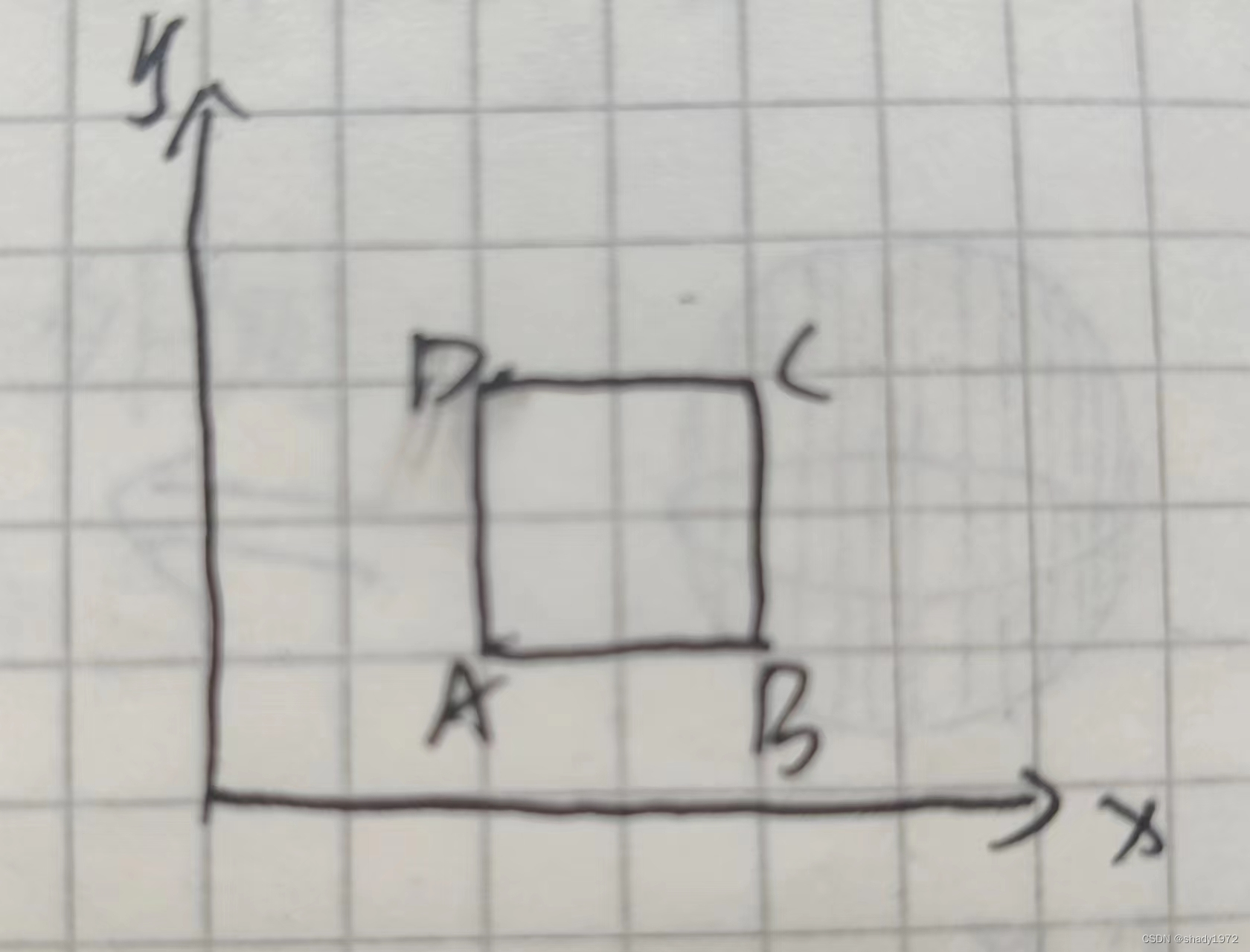
$\Phi$ EFGH = R(x,y,z+dz)dxdy

$\Phi$ BCFG = P(x+dx,y,z)dydz

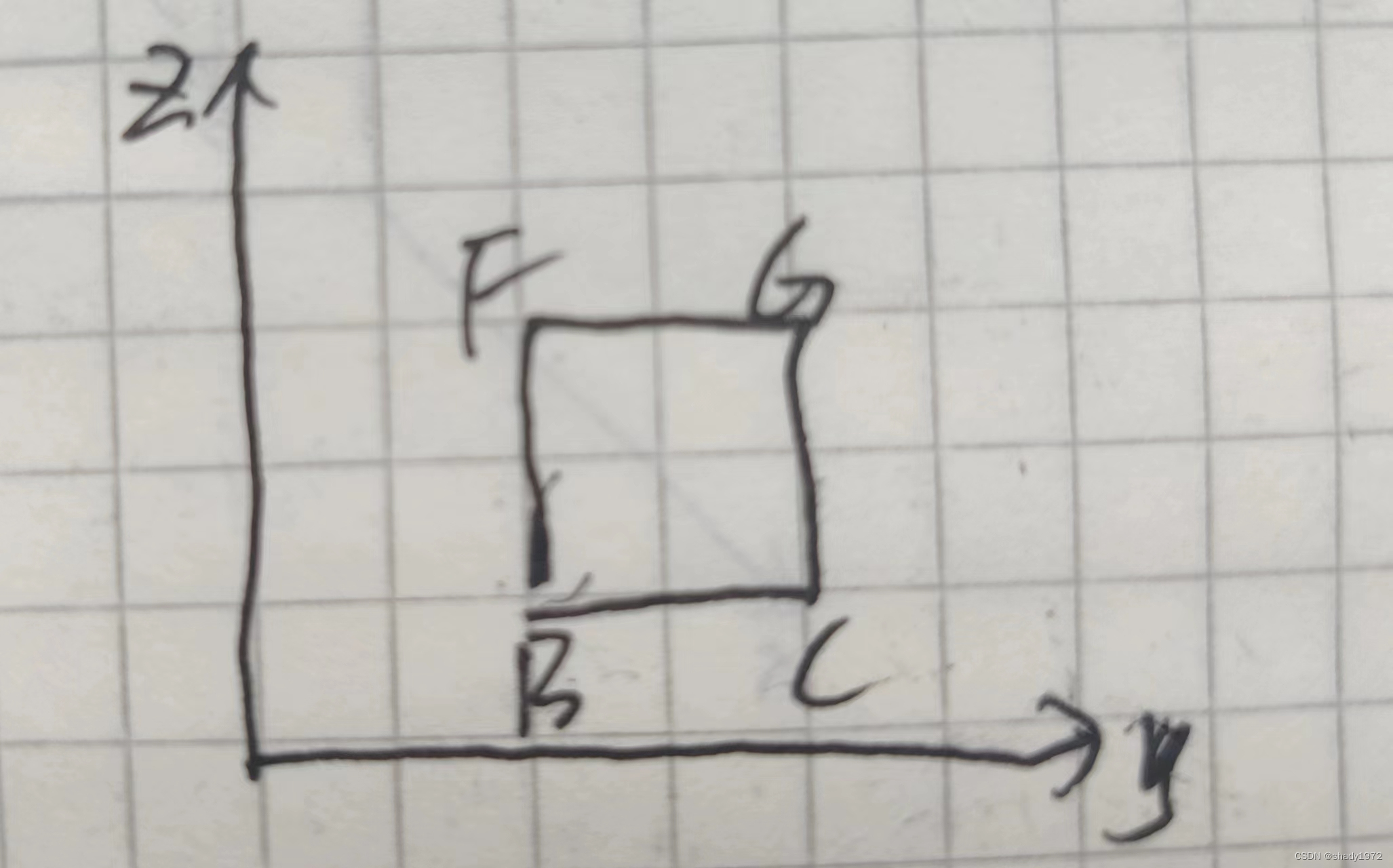
$\Phi$ ADEH = -P(x,y,z)dydz

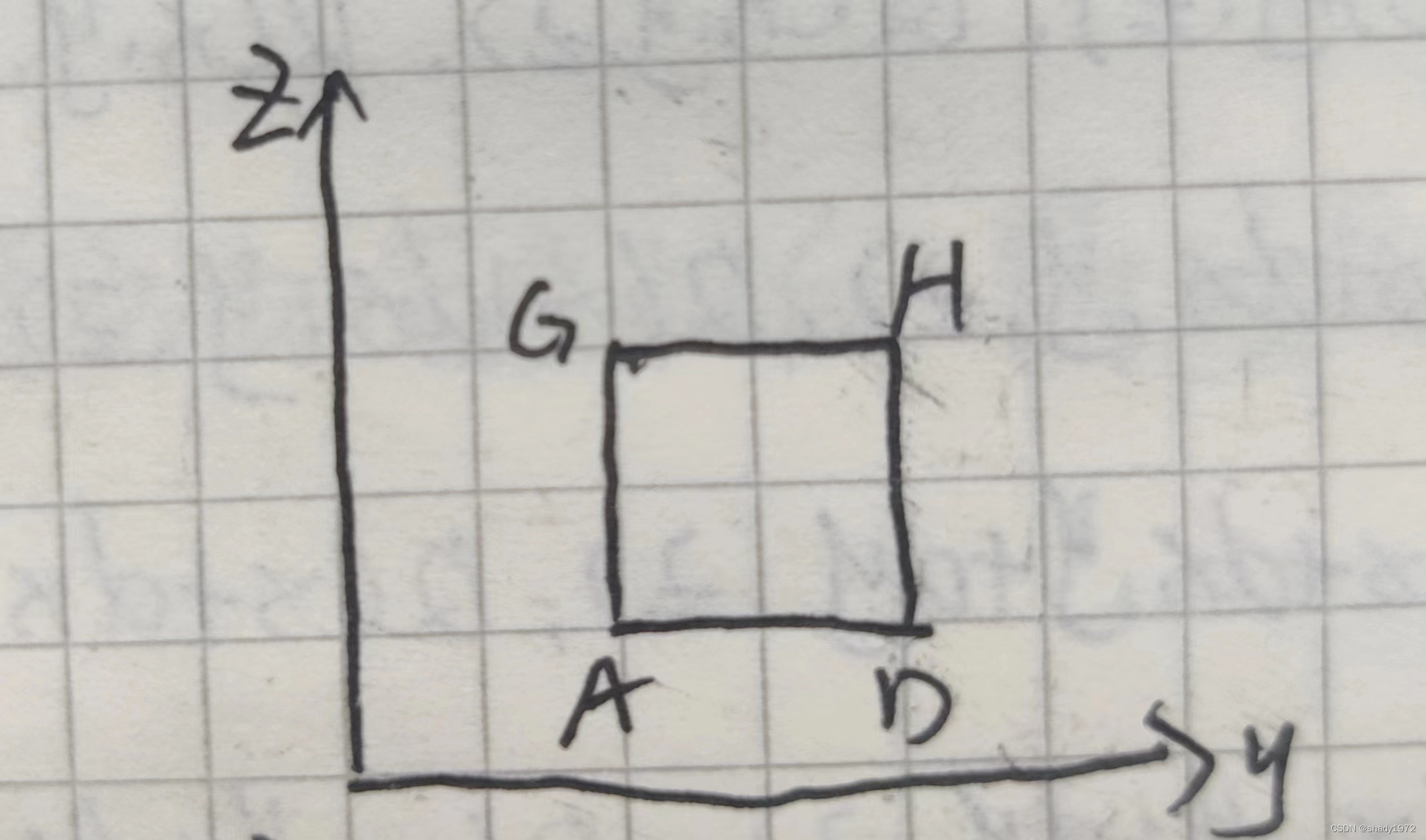
$\Phi$ ABEF = -Q(x,y,z)dxdz

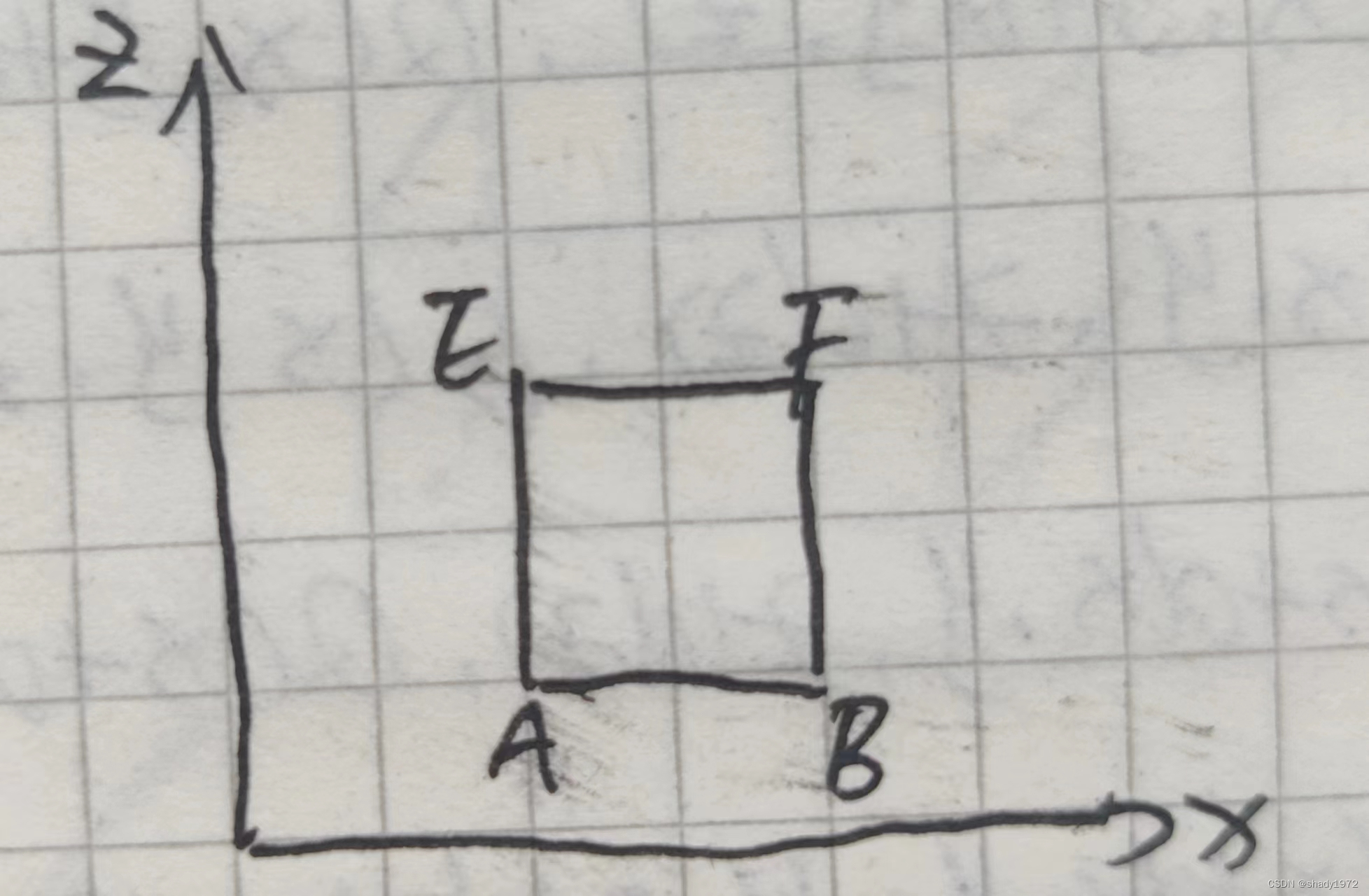
$\Phi$ DCHG = Q(x,y+dy,z)dxdz

再将全部加起来就是总通量

$\Phi$ = $\Phi$ ABCD + $\Phi$ EFGH + $\Phi$ BCFG + $\Phi$ ADEH + $\Phi$ ABEF + $\Phi$ DCHG

= $P(x+dx,y,z)dydz - P(x,y,z)dydz + Q(x,y+dy,z)dxdz - Q(x,y,z)dxdz + R(x,y,z+dz)dxdy -R(x,y,z)dxdy$

= $[P(x+dx,y,z) - P(x,y,z)]dydz + [Q(x,y+dy,z) - Q(x,y,z)]dxdz + [R(x,y,z+dz) -R(x,y,z)]dxdy$

= $\frac{P(x+dx,y,z) - P(x,y,z)}{{\partial }x{\partial }y{\partial }z}dy^{2}dz^{2}dx + \frac{Q(x,y+dy,z) - Q(x,y,z)}{{\partial }x{\partial }y{\partial }z}dx^{2}dz^{2}dy + \frac{R(x,y,z+dz) - R(x,y,z)}{{\partial }x{\partial }y{\partial }z}dx^{2}dy^{2}dz$

= $\frac{P(x+dx,y,z) - P(x,y,z)}{{\partial }x}dxdydz + \frac{Q(x,y+dy,z) - P(x,y,z)}{{\partial }y}dxdydz + \frac{R(x,y,z+dz) - P(x,y,z)}{{\partial }z}dxdydz$

= $\left ( \frac{\partial P(x,y,z))}{\partial x}+\frac{\partial Q(x,y,z))}{\partial y} + \frac{\partial R(x,y,z))}{\partial z} \right )dxdydz$

所以一个小块的通量就是 $\left ( \frac{\partial P(x,y,z))}{\partial x}+\frac{\partial Q(x,y,z))}{\partial y} + \frac{\partial R(x,y,z))}{\partial z} \right )dxdydz$

因为空间曲面围成的是空间几何体，所以将其进行三重积分

那么最后得到高斯公式

随之出现的 $\frac{\partial P(x,y,z))}{\partial x}+\frac{\partial Q(x,y,z))}{\partial y} + \frac{\partial R(x,y,z))}{\partial z}$ 也就是场论中一个重要的概念 散度 ,所以高斯定理也叫做散度定理。