个人做网站可以盈利么百度pc网页版入口
平台:matlab2021b,Vivado2018
应用场景和理解
一个早餐店,假如一天都有生意,生意有的时间很火爆,有时候又一般,老板又是个实在人,只知道在后厨蒸包子。由于包子蒸熟需要一定的时间,老板娘在前面卖包子。老板娘耍了一会儿手机,客人买包子的速度很快,一会儿包子就卖完了,老板娘给老板说包子卖完了。老板说马上包。这个问题就可以使用我们的公式来控制,老板娘如果不耍手机,隔几分钟就告诉老板现在还有多少包子。老板根据现在的情况来包包子,保证整体的数量恒定。根据这个例子来说明PID的含义,老板娘看剩余包子个数的频率为几分钟一次还是十几分钟一次。这个时间就是采样时间T。老板加包子有时候抱一笼出来,有时候抱几笼出来,一次拿一笼出来赶不上客人吃包子的速度,一次拿几笼出来,发现客人吃的慢,很久都不用拿出来。这个拿包子的笼数就是比例系数P。在加包子的过程中,有时候直接把蒸笼拿上去蒸,导致累的过高,老板娘取不下来。这时候把包子放在这里,让老板娘自己去把蒸笼放好。这里老板娘控制的放的方式就是积分时间I。后面有时候客人一次买很多包子,有些客人就买几个,老板有时候抱出来的包子太多了,有时候又抱出来的太少了,老板自己想了个办法,在半路上老板娘在看一眼,发现抱多了,就放一些回去,拿少了就再去抱一些出来。这个多少就是微分时间D。好了现在经过一系列的操作老板终于可以保证外面的包子稳定在一个恒定的个数上了。
算法公式
PID控制算法是一种闭环控制算法。在工业中被广泛应用。在PID系统框图中,整个系统包括比较器、PID控制器和控制对象,其中PID控制器包括三个模块,比例(P),积分(I)和微分(D)。

r(t)为系统的目标值,y(t)为系统的输出值。e(t)为系统目标值和输出值的偏差。
u(t)作为控制系统中的中间变量,既是偏差e(t)通过PID控制算法处理后的输出量。又是被控制对象的输入量。因此模拟PID控制器的公式为:
其中,为比例增益,
为积分时间常数,
为微分时间常数。
PID离散化算法公式
离散化的算法公式分为位置式PID算法和增量式算法。
位置式算法,假设采样时间间隔为T,则在k时刻:偏差为e(k);积分为e(k),e(k-1),e(k-2)…+e(0);微分时间为(e(k)-e(k-1))/T。离散化后的公式为
上式化简为
增量式PID算法
根据位置式可知
则
可以得出
以上就是增量式算法,由增量式算法公式可知,系统的增量只和进三次偏差有关系。
由上述公式特点可以分析出来。位置式公式,需要多每次的误差进行累加,每次的输出都和过去的状态有关系。而增量式公式,误差只与最近三次采集有关系。但是积分影响大,稳态误差。
下面我们将通过matlab仿真对该公式进行分析,详细分析两种公式的参数影响。
先看位置式PID
clc;
clear;PID_target = 24; % 目标温度为24摄氏度% 定义PID三个参数的初始值
Kp = 0.01;
Ki = 0;
Kd = 0;% 定义误差
ek = 0;
ek_1 = 0;
ek_sum = 0;
sum_threshold = 8; % 阈值设定为8% PID输出
PID_out = 0;% 数据采集点数
numPoints = 200;% 采集初始值
ADC_data = zeros(1,numPoints);% 存储PID输出数据
PID_out_data = zeros(1, numPoints);
PID_target_data = PID_target * ones(1, numPoints);% 计算PID输出
for t = 4:numPointsek = PID_target - ADC_data(t-3);if (t>=12)ek_sum = ek_sum - ek_sum/sum_threshold;endek_sum = ek_sum+ek;PID_out = PID_out + Kp * ek + Ki * ek_sum + Kd * (ek - ek_1);ek_1 = ek;
% ADC_data(t) = PID_out + randn(1); % 添加随机噪声ADC_data(t) = PID_out; PID_out_data(t) = PID_out;
end% 绘制PID_out和PID_target的图像
figure;
hold on;
plot(1:numPoints, PID_out_data, 'b', 'LineWidth', 1.5);
plot(1:numPoints, PID_target_data, 'r--', 'LineWidth', 1.5);
hold off;
title('PID输出与目标值变化图像');
xlabel('时间步数');
ylabel('数值');
legend('PID输出', '目标值', 'Location', 'best');在应用过程中对误差累积求和往往往往不需要进行全部累加。这里代码中只累加了8次。采集值我这里做了延迟响应,即PID调整三个值后在响应第一个点。这样就模拟了外部的响应时间。这里我们将调节目标设置在10个点左右到达稳定值。
设置初始值P=0.01;I=0;D=0;

调节时间明显过长。
设置值P=0.1;I=0;D=0;

缩短了调节时间但是不够。
设置值P=0.2;I=0;D=0;
 调节时间满足了但是有点过冲了。这里看一下积分项I的作用,稍微增大一点点。
调节时间满足了但是有点过冲了。这里看一下积分项I的作用,稍微增大一点点。
设置值P=0.2;I=0.005;D=0;

可以看到过冲更加明显了。
设置值P=0.2;I=0.005;D=0.01;

尝试使用微分将过冲调节下来。适当增大微分项。
设置值P=0.2;I=0.005;D=0.2;

减小了一点点。但是减不下去。
设置值P=0.2;I=0.0005;D=0.2;在减少积分项将过冲拉低。

可以看到波形过冲消失,但是不够平滑。
适当的缩小I微分参数,可以将波形调整到很平滑的位置。差不多达到我们预计的要求。
设置值P=0.2;I=0.0005;D=0.1;

再看增量式PID
clc;
clear;PID_target = 24; % 目标温度为24摄氏度% 定义PID三个参数的初始值
Kp = 0.01;
Ki = 0.01;
Kd = 0.01;% 定义误差
ek = 0;
ek_1 = 0;
ek_2 = 0;% PID输出
PID_out = 0;% 采集初始值
ADC_data = 0;% 数据采集点数
numPoints = 200;% 采集初始值
ADC_data = zeros(1,numPoints);% 存储PID输出数据
PID_out_data = zeros(1, numPoints);
PID_target_data = PID_target * ones(1, numPoints);% 计算PID输出
for t = 4:numPointsek = PID_target - ADC_data(t-3);PID_out = PID_out + Kp * (ek - ek_1) + Ki * ek + Kd * (ek - 2 * ek_1 + ek_2);ek_2 = ek_1;ek_1 = ek;
% ADC_data(t) = PID_out + randn(1); % 添加随机噪声ADC_data(t) = PID_out ; % 添加随机噪声PID_out_data(t) = PID_out;
end% 绘制PID_out和PID_target的图像
figure;
hold on;
plot(1:numPoints, PID_out_data, 'b', 'LineWidth', 1.5);
plot(1:numPoints, PID_target_data, 'r--', 'LineWidth', 1.5);
hold off;
title('PID输出与目标值变化图像');
xlabel('时间步数');
ylabel('数值');
legend('PID输出', '目标值', 'Location', 'best');设置初始值
设置初始值P=0.01;I=0.01;D=0.01;

适当增加比例系数P=0.2;I=0.01;D=0.01;

波形调节无明显变化。前面说到增量式积分项对响应时间影响较大,这里适当增加积分项。
P=0.2;I=0.1;D=0.01;

继续增加积分项到满足调节时间P=0.2;I=0.26;D=0.01;

满足了调节时间有了过冲,适当P=0.2;I=0.26;D=0.1;

可以看到波形在接近目标值的时候震荡。继续调整参数。发现要到达预定的响应时间,波形不会平滑。笔者又尝试了一些参数。
最后P=0.01;I=0.17;D=0.01;波形接近稳定,但是没有达到预计的响应时间。
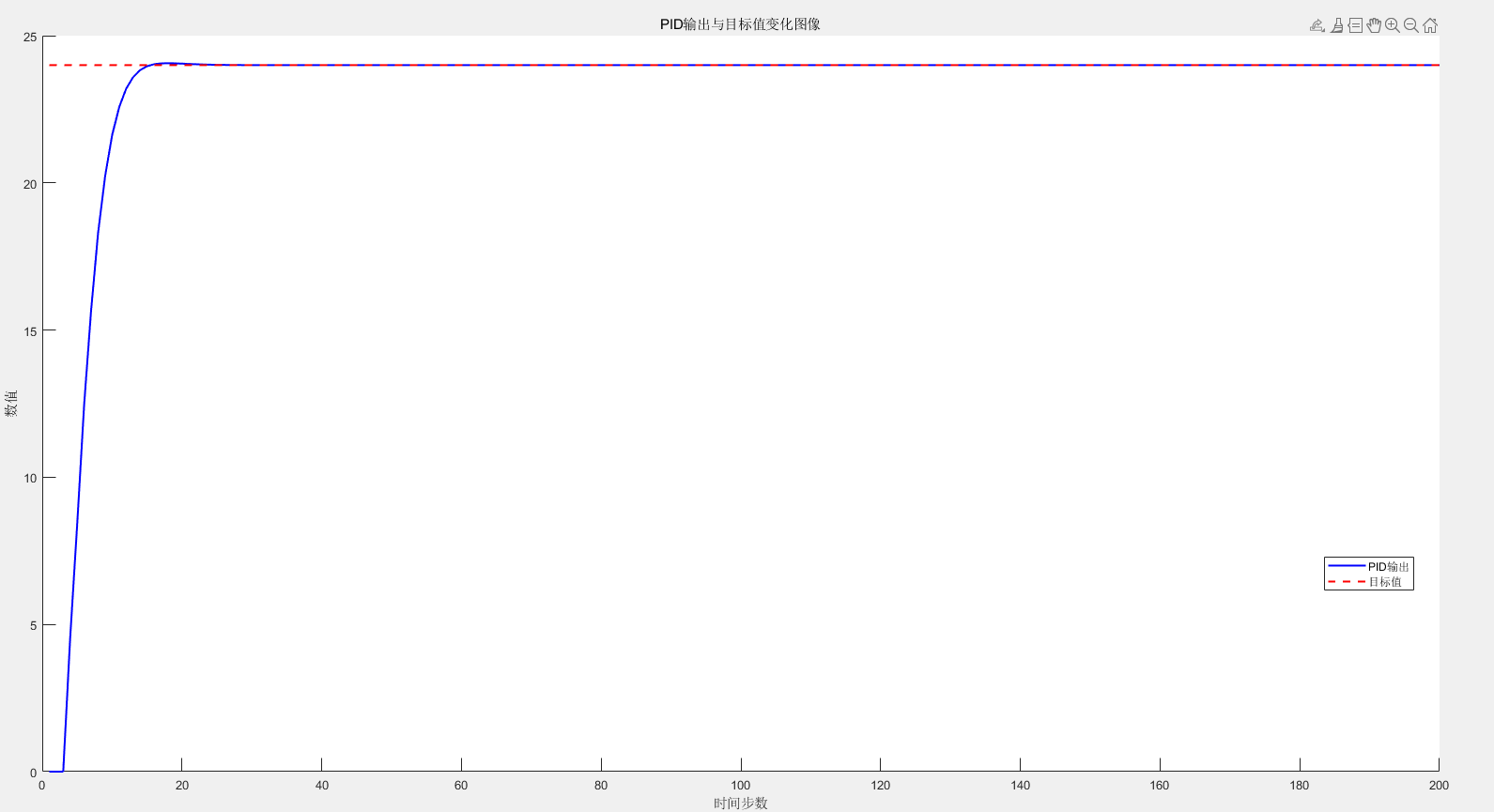
从上面可以看出来位置式相对增量式可以更快更稳定的达到响应时间。且位置式的参数的作用和增量式参数的作用在调试的过程中有一点点差别。从实现方式来看,增量式的计算量明显更小。
参考
演示PID三个参数的控制作用 (qq.com)
