做二手网站好的名字app拉新接单平台

 滤波的可分离性

     就是将一个线性滤波变成多个线性滤波，这里面具体所指的是变成x方向的线性滤波和y方向的线性滤波。无论先做x方向的滤波还是y方向滤波，两者的叠加结果是一致的，这个性质取决于滤波操作是并行的，也就是每一个图像在滤波的时候，图像滤波区域内的像素是独立进计算的，如果性能允许，我们可以在整个图像内同时计算。

可分离滤波的含义

线性滤波可以将滤波器分解为x方向和y方向两个滤波器，并且滤波结果与顺序无关。

     比如现在有行滤波器和列滤波器，这两个滤波器分别作用在图像中，比如先用行滤波器进行处理，之后再进行列滤波器对图像进行处理，得到的结果与行和列滤波器乘在一起的整体（联合)滤波器对图像进行滤波所得到的结果是一致的。

      进行滤波器分离后，好处是滤波时采用的数据变少了，因为进行行滤波时，使用的是三个数据，进行列滤波时，使用的是三个数据，而如果直接用联合滤波器使用的是九个数据，从上可知，分离滤波可以极大缩减滤波处理时间，同时也为cpu这种串行处理器上实现滤波加速成为可能。

高斯滤波器用分离形式表示:

      可表示成一个列滤波器和一个行滤波器，这两个滤波器的乘积可得到一个联合(整体)滤波器。若先对第一个列滤波器对图像进行操作，得到结果后，再将此结果输入到下一个行滤波器中，得到的最终结果与图像直接输入到联合滤波器中的结果是一致的。这样的形式可以实现两个方向上不同的滤波，例如在行上用5*5尺寸的滤波器，而在列上用3*3尺寸的滤波器，这样可以增大灵活性。

可分离滤波函数

sepFilter2D()

void cv::sepFilter2D(InputArray    src,OutputArray   dst,int           ddepth,InputArray    kernelX,InputArray    kernelY,Point         anchor = Point(-1,-1),double        deta = 0;int           borderType = BORDER_DEFAULT)

·src:待滤波图像。

·dst:输出图像，与输入图像src具有相同的尺寸，通道数和数据类型。

·ddepth:输出图像的数据类型（深度）,可以通过此参数修改输出图像的数据类型，因为滤波与卷积相类似，卷积过程中 可能在求和时使数据变得更大，例如方框滤波，所得结果远大于原先数据，若此时还使用原数据类型，那么可能会造成数据丢失，因此允许从此参数去设置输出的数据类型。

·kernelX:X方向的滤波器。

·kernelY:Y方向的滤波器。

·anchor:内核的基准点（锚点），其默认值为（-1，-1）代表内核基准点位于kernel的中心位置。

·delta:偏值，在计算结果上加上偏值。

·borderType:像素外推法选择标志。

示例

#include <opencv2/opencv.hpp>
#include <iostream>using namespace cv; //opencv的命名空间
using namespace std;//主函数
int main()
{float points[25] = { 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25 };Mat data(5, 5, CV_32FC1, points);//X方向，Y方向和联合滤波器的构建Mat a = (Mat_<float>(3, 1) << -1, 3, -1);Mat b = a.reshape(1, 1);//将3*1的矩阵变为1*3的通道的矩阵Mat ab = a * b;//验证高斯滤波的可分离性Mat gaussX = getGaussianKernel(3, 1); //此函数可自动生成一定尺寸的高斯滤波器,第一个参数是尺寸，第二个参数是标准差Mat gaussData, gaussDataXY;GaussianBlur(data, gaussData, Size(3, 3), 1, 1, BORDER_CONSTANT);sepFilter2D(data, gaussDataXY, -1, gaussX, gaussX, Point(-1, -1), 0, BORDER_CONSTANT);//输入两种高斯滤波的计算结果cout << "gaussData=" << endl << gaussData << endl;cout << "gaussDataXY=" << endl << gaussDataXY << endl;//线性滤波的可分离性Mat dataYX, dataY, dataXY, dataXY_sep;filter2D(data, dataY, -1, a, Point(-1, -1), 0, BORDER_CONSTANT); //进行y方向滤波filter2D(dataY, dataYX, -1, b, Point(-1, -1), 0, BORDER_CONSTANT); //进行x方向滤波filter2D(data,dataXY, -1, ab, Point(-1, -1), 0, BORDER_CONSTANT); //xy联合滤波，此结果应当与前两个操作的结果一致sepFilter2D(data, dataXY_sep, -1, b, b, Point(-1, -1), 0, BORDER_CONSTANT); //使用分离滤波函数进行滤波的结果,若与上面的结果一致，那么可以得到结论：分离滤波函数可以接受两个同尺寸的滤波器//输出分离滤波和联合滤波的计算结果cout << "dataYX=" << endl << dataYX << endl;cout << "dataXY=" << endl << dataXY << endl;cout << "dataXY_sep=" << endl << dataXY_sep << endl;//对于图像的可分离操作Mat img = imread("E:/opencv/opencv-4.6.0-vc14_vc15/opencv/lenac.png");if (img.empty()){cout << "请确认图像文件名是否正确" << endl;}Mat imgYX, imgY, imgXY;filter2D(img, imgY, -1, a, Point(-1, -1), 0, BORDER_CONSTANT);filter2D(imgY, imgYX, -1, b, Point(-1, -1), 0, BORDER_CONSTANT);filter2D(img, imgXY, -1, ab, Point(-1, -1), 0, BORDER_CONSTANT);imshow("img", img);imshow("imgY", imgY);imshow("imgYX", imgYX);imshow("imgXY", imgXY);waitKey(0);//等待函数用于显示图像,按下键盘任意键后退出return 0;}

结果

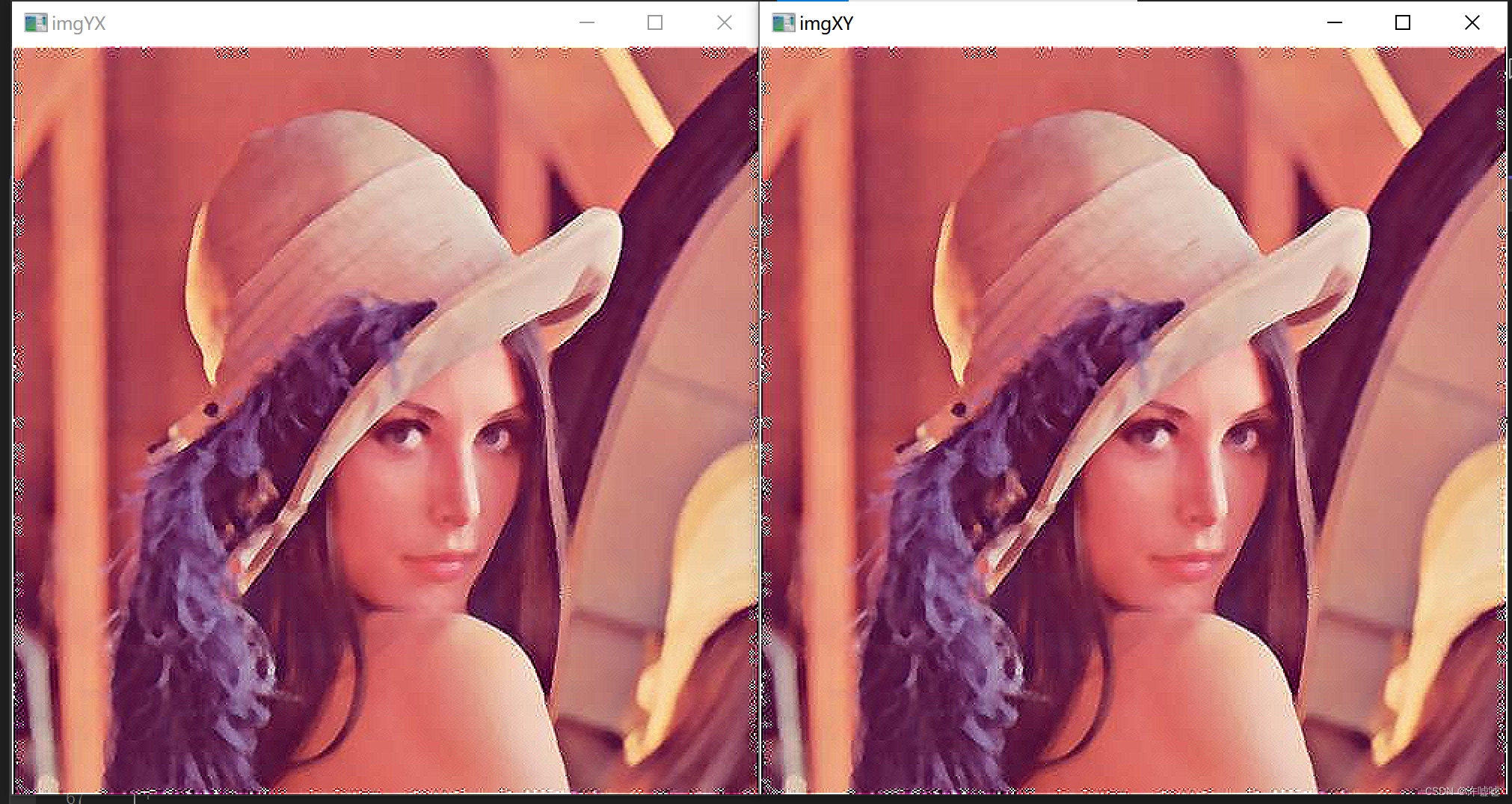 由运行结果可知，对于图像的滤波可以经过线性分离实现，这样可以极大的所见程序运行所需要的数据，我们不需要将两个方向的滤波器乘在一起得到联合滤波器，也缩减了我们的工作量。