毕业设计做网站难吗内容营销平台有哪些

前言

不是学电子出身的，这里很多东西是问了朋友…

模拟域中的一阶低通滤波器传递函数

模拟域中的一阶低通滤波器的传递函数可以表示为：

$$H(s)=\frac{1}{s+{\omega }_c}$$

这是因为一阶低通滤波器的设计目标是允许低频信号通过，同时衰减高频信号。具体来说，它的频率响应特性决定了这个形式的传递函数。

1. 传递函数的来源

一阶低通滤波器的传递函数来源于它的微分方程描述。考虑一个简单的RC（电阻-电容）电路：

• 电阻 $R$
• 电容 $C$
  

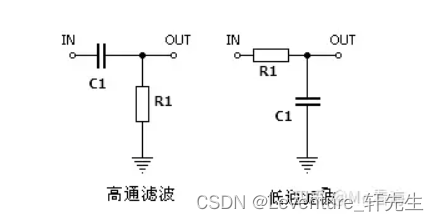
高通滤波器

对于高通滤波器电路（左图），我们有一个电容 $C_1$ 和一个电阻 $R_1$：

1. 阻抗计算：

   • 电容的阻抗 $Z_C=\frac{1}{j\omega C_1}$
   • 电阻的阻抗 $Z_R=R_1$

2. 电路分析：

   • 输入电压 $V_{in}$ 加在电容和电阻的串联上。
   • 输出电压 $V_{out}$ 在电阻上。

使用分压公式：

$$V_{out}=V_{in}\cdot \frac{Z_R}{Z_R+Z_C}=V_{in}\cdot \frac{R_1}{R_1+\frac{1}{j\omega C_1}}=V_{in}\cdot \frac{R_1\cdot j\omega C_1}{1+j\omega R_1{C}_1}$$

所以，传递函数 $H(s)$ 是：

$$H(s)=\frac{V_{out}}{V_{in}}=\frac{j\omega R_1{C}_1}{1+j\omega R_1{C}_1}=\frac{s{R}_1{C}_1}{1+s{R}_1{C}_1}$$

令 ${\omega }_c=\frac{1}{R_1{C}_1}$，则传递函数为：

$$H(s)=\frac{s/{\omega }_c}{1+s/{\omega }_c}$$

低通滤波器

对于低通滤波器电路（右图），我们有一个电阻 $R_1$ 和一个电容 $C_1$：

1. 阻抗计算：

   • 电阻的阻抗 $Z_R=R_1$
   • 电容的阻抗 $Z_C=\frac{1}{j\omega C_1}$

2. 电路分析：

   • 输入电压 $V_{in}$ 加在电阻和电容的串联上。
   • 输出电压 $V_{out}$ 在电容上。

使用分压公式：

$$V_{out}=V_{in}\cdot \frac{Z_C}{Z_R+Z_C}=V_{in}\cdot \frac{\frac{1}{j\omega C_1}}{R_1+\frac{1}{j\omega C_1}}=V_{in}\cdot \frac{1}{j\omega R_1{C}_1+1}$$

所以，传递函数 $H(s)$ 是：

$$H(s)=\frac{V_{out}}{V_{in}}=\frac{1}{1+j\omega R_1{C}_1}=\frac{1}{1+s{R}_1{C}_1}$$

令 ${\omega }_c=\frac{1}{R_1{C}_1}$，则传递函数为：

$$H(s)=\frac{1}{1+s/{\omega }_c}$$

微分方程形式

这个电路的微分方程可以写为：

$$V_{out}(t)=\frac{1}{RC}{\int }_{-\infty }^t{V}_{in}(\tau )e^{-\frac{t-\tau }{RC}}d\tau$$

通过拉普拉斯变换，将其转化到频域：

$$\frac{V_{out}(s)}{V_{in}(s)}=\frac{1}{RC\cdot s+1}$$

令 ${\omega }_c=\frac{1}{RC}$，得到：

$$H(s)=\frac{1}{s+{\omega }_c}$$

2. 频率响应

一阶低通滤波器的传递函数 $H(s)$ 表示了滤波器对不同频率信号的响应：

• 当 $s=j\omega$ 时，低频（$\omega$ 较小）信号通过的幅度接近 1，即通过率高。
• 当 $\omega$ 较大时，传递函数的值接近 0，即高频信号被大大衰减。

3. 截止频率

${\omega }_c$ 是滤波器的截止频率，即在该频率处信号的幅度被衰减到原来的 $\frac{1}{\sqrt{2}}$ 倍（约 0.707 倍）。它定义了低通滤波器允许通过的最大频率。

综上所述，模拟域中的一阶低通滤波器传递函数为：

$$H(s)=\frac{1}{s+{\omega }_c}$$

是由其设计目标、微分方程描述以及频率响应特性决定的。

二阶滤波器通过联级一阶滤波器的推导

二阶滤波器可以通过两个一阶滤波器串联（联级）得到。假设我们有两个一阶低通滤波器，其传递函数分别为：

$$H_1(s)=\frac{1}{1+s/{\omega }_{c1}}$$

$$H_2(s)=\frac{1}{1+s/{\omega }_{c2}}$$

当将这两个一阶滤波器串联时，总的传递函数 $H(s)$ 为：

$$H(s)=H_1(s)\cdot H_2(s)$$

即：

$$H(s)=\left(\frac{1}{1+s/{\omega }_{c1}}\right)\cdot \left(\frac{1}{1+s/{\omega }_{c2}}\right)$$

假设两个一阶滤波器的截止频率相同，即 ${\omega }_{c1}={\omega }_{c2}={\omega }_c$，则总的传递函数为：

$$H(s)={\left(\frac{1}{1+s/{\omega }_c}\right)}^2$$

将其展开得到：

$$H(s)=\frac{1}{(1+s/{\omega }_c{)}^2}=\frac{1}{1+\frac{2s}{{\omega }_c}+{\left(\frac{s}{{\omega }_c}\right)}^2}$$

这就是一个标准的二阶低通滤波器的传递函数形式。它可以表示为：

$$H(s)=\frac{1}{1+\frac{2s}{{\omega }_c}+{\left(\frac{s}{{\omega }_c}\right)}^2}$$

或者更一般的形式：

$$H(s)=\frac{{\omega }_c^2}{s^2+2\zeta {\omega }_{c}s+{\omega }_c^2}$$

其中，$\zeta$ 是阻尼系数，对于上述情况 $\zeta =1$。通过改变 $\zeta$ 的值，可以设计出具有不同频率特性的二阶滤波器。

总结

通过将两个一阶低通滤波器串联，我们得到了一个二阶低通滤波器的传递函数。这个方法可以推广到高通、带通和带阻滤波器，通过适当的组合一阶滤波器可以实现各种复杂的频率响应特性。